Histogram en steel-bladdiagram (H6.3) - G&R 12de - VWO 2

     ( Wiskunde - Getal en Ruimte 12de editie, VWO 2 , H6. Procenten en diagrammen)

H6.3 Histogram en steel-bladdiagram

(Opgave 36, 37, 39, 41, 44)

Opgave 36.

a.

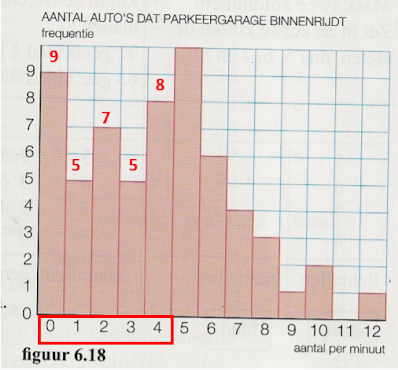
→ Het bovenstaande histogram geeft gegevens over het aantal auto's dat per minuut een parkeergarage binnenrijdt.

• 1 keer 9 auto's per minuut + 2 keer 10 auto's per minuut + 1 keer 12 auto's per minuut = 4 keer dat er meer dan acht auto's per minuut binnenreden.

b.

→ 9 + 5 + 7 + 5 + 8 + 10 + 6 + 4 + 3 + 1 + 2 + 1 = 61 minuten

c.

→ (5 × 1) + (7 × 2) + (5 × 3) + (8 × 4) + (10 × 5) + (6 × 6) + (4 × 7) +(3 × 8) + (1 × 9) + (2 × 10) + (1 × 12) = 5 + 14 + 15 + 32 + 50 + 36 + 28 + 24 + 9 +20 + 12 = 245 auto's

d.

→ Het aantal keren dat er minder dan vijf auto's per minuut binnen kwamen = 9 + 5 + 7 + 5 + 8 = 34 

→ Percentage keren dat er minder dan vijf auto's per minuut binnen kwamen = 34 ÷ 61 × 100% = 55,7%

Opgave 37.

a.

→ Meneer Braamhaar heeft in een periode bijgehouden hoeveel verkeerslichten per dag op rood stonden.

→ "De frequentie van het waarnemingsgetal 5 is 6" betekent dat in de periode het aantal dagen waarop er 5 verkeerslichten op rood stonden, 6 is.

b.

→ Het aantal dagen dat meneer Braamhaar meer dan zes keer voor een verkeerslicht wacht = 6 + 1+ 1 = 8

c.

→ 4 + 4 + 6 + 8 + 6 + 1 + 1 = 30 dagen

→ Het aantal werkdagen per week is 5.

→ 30 dagen ÷ 5 = 6 weken

d.

→ Dat in de bovenste regel van de frequentietabel de getallen 0, 1 en 2 niet voorkomen betekent dat meneer Braamhaar in de periode elke dag meer dan 2 keer voor een verkeerslicht moest wachten.

e.

f.

→ (3 × 4) + (4 ×4 ) + (5 × 6) + (6 × 8) + (7 × 6) + (8 × 1) + (9 × 1) = 165 keer

Opgave 39

a.

• 17 twee keer
• 21 twee keer
• 23 drie keer
• 28 nul keer

b.

→ De hoogst behaalde score is 41.

c.

→ Aantal leerlingen die de test hebben gemaakt = 3 + 6 + 6 + 3 + 2 = 20

Opgave 41.

a.

→ Als je aan de mannenkant het aantal telt: 14 beroepen.

→ Als je aan de vrouwenkant het aantal telt: 14 beroepen.

→ In het steel-bladdiagram is het uurloon verwerkt van 14 beroepen.

b.

→ Bij mannen worden de beroepen van office-manager en arbeidsbemiddelaar gelijk betaald.

→ In het diagram aan de mannenkant zie je bij tienden hetzelfde getal bij twee beroepen met 12 eenheden. Dat is 0.

→ Het gemiddelde uurloon van mannen bij de beroepen van office-manager en arbeidsbemiddelaar is  € 12,00 per uur. 

c.

→ Bij de meeste beroepen verdienen mannen meer dan vrouwen. Zo verdient een mannelijke werkvoorbereider per uur € 0,60 meer dan zijn vrouwelijke collega.

→ Het verschil van € 0,60 tussen uurloon voor mannen en uurloon voor vrouwen zie je in 2 gevallen:

• Eerste geval:  uurloon € 14,80 voor mannen en uurloon € 14,10 voor vrouwen
• Tweede geval: uurloon € 14,20 voor mannen en uurloon € 13,60 voor vrouwen

• € 13,60 + € 0,60 =  € 14,20 
• € 14,10 + € 0,60 =  € 14,70 

→ Het uurloon van een mannelijke werkvoorbereider is € 14,20 of € 14,70.

d.

→ Zoek eerst hetzelfde getal bij de tienden bij mannen en vrouwen.

→ Daarna kijk je of het verschil tussen de twee getallen bij de eenheden met hetzelfde getal bij de tienden bij mannen en vrouwen, 5 is.

→ Het uurloon van een vrouwelijk hoofd facilitaire dienst is € 19,80 per uur. 

e.

→ Het aantal beroepen waarbij een vrouw in een week van 36 uur minder dan 525 euro verdient:

• Het weekloon van een vrouw die € 14,80 per uur verdient is  € 14,80 × 36 = 532,8 euro
• Het weekloon van  een vrouw die € 14,10 per uur verdient is  € 14,10 × 36 = 507,6 euro
• Het aantal beroepen waarbij een vrouw in een week minder dan 525 euro verdient is 10.

→ Het percentage van de in het diagram verwerkte beroepen die voor een vrouw in een week minder dan 525 euro opleveren = 10 ÷ 14 ×100% ≈ 71,4% (rond procenten af op één decimaal).

Opgave 44.

a.

b.

c.

→  Het aantal leerlingen die minder dan 15 kwartier aan het huiswerk besteed hebben, is 1 + 4 + 5 = 10

→ Het ootale aantal leerlingen van klas V2C is 1 + 4 + 5 + 7 + 5 + 2 + 3 = 27

→ Het percentage van de leerlingen die minder dan 15 kwartier aan het huiswerk besteed hebben = 10 ÷ 27 × 100% ≈ 37,0% (rond procenten af op één decimaal).

d.

→ 6 uur is 4 kwartier × 6 = 24 kwartier

→ Het aantal leerlingen die meer dan 24 kwartier aan het huiswerk besteed hebben, is 2 + 3 = 5

→ Het totale aantal leerlingen van klas V2C is 1 + 4 + 5 + 7 + 5 + 2 + 3 = 27

→ Het percentage van de leerlingen die meer dan 24 kwartier (= 6 uur) aan het huiswerk besteed hebben = 5 ÷ 27 × 100% ≈ 18,5% (rond procenten af op één decimaal).