Gemengde opgaven - H8 Inhoud en vergroten - G&R 12de - VWO 2

      (Wiskunde - Getal en Ruimte 12de editie, VWO 2 , H8. Inhoud en vergroten)

Gemengde Opgaven H8. 

(Opgave 1, 2, 3, 5, 6, 7)

Opgave 1.

a.

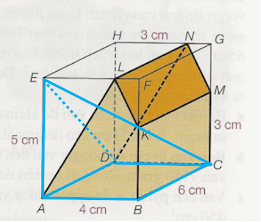
 (Elk prisma heeft twee evenwijdige zijvlakken: het grondvlak en het bovenvlak. Je ziet dat het grondvlak niet altijd aan de onderkant zit.)

→ Het grondvlak van het prisma is :

→ De oppervlakte van het grondvlak van het prisma wordt berekend als volgt:

•      (5 × 4 ) – {(½ × 5 × 3) +  (½ × 1 × 2)} = 20 – 8,5 = 11,5 cm²

→ De hoogte van het prisma is 6 cm.

• inhoud prisma = oppervlakte grondvlak × hoogte
• de inhoud van het prisma = 11,5 × 6 = 69 cm³

b.

→ De piramide E ABCD is:

→  De inhoud van de piramide E ABCD wordt berekend als volgt:

• inhoud piramide = ⅓ × oppervlakte grondvlak × hoogte
• de oppervlakte van het grondvlak van de piramide E ABCD = 4 × 6 = 24 cm²
• de hoogte van de piramide is 5 cm
• de inhoud van de piramide E ABCD = ⅓ × 24 × 5 = 40 cm³ 

c.

→ De piramide E KMGF is:

→ De inhoud van de piramide E KMGF wordt berekend als volgt:

• inhoud piramide = ⅓ × oppervlakte grondvlak × hoogte
• de oppervlakte van het grondvlak van de piramide E KMGF = 6 × 2 = 12 cm²
• de hoogte van de piramide is 4 cm.
• de inhoud van de piramide E KMGF = ⅓ × 12 × 4 = 16 cm³

d.

→ Joost plaatst in een balk van 4 bij 5 bij 6 cm een zo groot mogelijke cilinder. 

→ Om de cilinder zo groot mogelijk te laten zijn, moet de diameter van de cilinder zo groot zijn als één van de ribben van de balk. Joost kan twee mogelijkheden vergelijken: 

• een cilinder waarvan de diameter 4 cm is en de hoogte 5 cm
• een cilinder waarvan de diameter 5 cm is en de hoogte 4 cm. 

① Een cilinder waarvan de diameter 4 cm is en de hoogte 5 cm

• de inhoud van deze cilinder = π × 2² × 5 ≈ 62,83

② Een cilinder waarvan de diameter 5 cm is en de hoogte 4 cm. 

• de inhoud van deze cilinder = π × 2,5² × 4 ≈ 78,5398

→ De inhoud van cilinder ① is kleiner dan de inhoud van cilinder ②

→ Cilinder ② is zo groot mogelijk gegeven de balk. De inhoud van cilinder ② is 78,5 cm³ (rond af op één decimaal).

Opgave 2.

a.

→  De inhoud van een messenblok = de inhoud van het bovenste prisma + de inhoud van het onderste prisma

① de inhoud van het bovenste prisma

• inhoud prisma = oppervlakte grondvlak × hoogte
• de oppervlakte van het grondvlak van het bovenste prisma = ½ × (1,4 dm + 0,6 dm) × 2,5 dm = 2,5 dm²
• de hoogte van het bovenste prisma = 1,2 dm
• de inhoud van het bovenste prisma = 2,5 dm² × 1,2 dm = 3 dm³.

      (Je kan ook de berekening in cm maken en daarna van cm³ naar dm³ omrekenen.)

• de oppervlakte van het grondvlak van het bovenste prisma = ½ × (14 cm + 6 cm) × 25 cm = 250 cm²
• de hoogte van het bovenste prisma = 12 cm
• de inhoud van het bovenste prisma = 250 cm² × 12 cm = 3.000 cm³
• 1000 cm³ = 1 dm³
• 3000 cm³ = 3 dm³

② de inhoud van het onderste prisma

• inhoud prisma = oppervlakte grondvlak × hoogte
• de oppervlakte van het grondvlak van het onderste prisma = ½ × 8 cm × 20 cm = 80 cm²
• de hoogte van het onderste prisma = 12 cm
• de inhoud van het onderste prisma = 80 cm² × 12 cm = 960 cm³
• 1000 cm³ = 1 dm³
• 960 cm³ = 0,96 dm³
• de inhoud van het onderste prisma = 960 cm³ = 0,96 dm³

③ De inhoud van het messenblok = 3 dm³ + 0,96 dm³ = 3,96 dm³

b.

→ De sleuven in het blok vormen 5% van de inhoud van het blok. Het hout weegt 1200 kg per m³.

→ Het gewicht van het hout is uitgedrukt in m³. 3,96 dm³, de inhoud van het messenblok, moet naar m³ omgerekend worden.

• 1000 dm³ = 1 m³
• 3,96 dm³ = 0,00396 m³

→ Het hout weegt 1200 kg per m³. De inhoud van 0,00396 m³ weegt 1200 kg × 0,00396 m³ =  4,752 kg

→ De sleuven in het blok vormen 5% van de inhoud van het blok.

• 5% × 4,752 kg = 0,2376 kg

→ Het gewicht van het messenblok = 4,752 kg – 0,2376 kg = 4,5144 kg

• Het gewicht van het messenblok is 4,5 kg (rond af op één decimaal).

c.

→ Van een ander messenblok zijn de afmetingen de helft van die van het gegeven blok. 

• Het andere messenblok is een verkleining van het gegeven messenblok. De vergrotingsfactor k is ½ (=0,5).

→ De vraag is hoeveel gram het kleine messenblok weegt. Het gewicht is gekoppeld aan de inhoud.

• inhoud beeld = k³ × inhoud origineel
• het gewicht van het kleine messenblok = 0,5³ × 4,5144 kg = 0,5643 kg
• 0,5643 kg = 564,3 gram

→ Het kleine messenblok weegt 564 gram (rond af op gehelen).

Opgave 3.

a.

→ inhoud cilinder = π × straal² × hoogte

→ De inhoud van de cilindervormige pijler = π × 10² × (40 + 18) = π × 10² × 58 ≈ 18221,2374

→ De inhoud van de cilindervormige pijler is 18.221 m³ (bereken in gehele m³).

b.

→ inhoud kegel = ⅓ × π × straal² × hoogte

→ de inhoud van het reservoir = ⅓ × π × (92 ÷ 2)² × (64,8 + 18) = ⅓ × π × 46² × 82,8 ≈183474,03

→ De inhoud van het reservoir is 183.474 m³ (rond af op gehelen).

Opgave 5.

• De drie formaten dozen zijn gelijkvormig.
• Formaat A: 150 gram drop kan in deze doos zitten en de lengte  van deze doos is 8 cm.
• Formaat B: 540 gram drop kan in deze doos zitten.
• Het gewicht is gekoppeld aan de inhoud.

a.

→ Om de lengte van een doos van formaat B te berekenen, moet je eerst de vergrotingsfactor k hebben.

• inhoud beeld = k³ × inhoud origineel
• k = ³√(inhoud beeld ÷ inhoud origineel)
• Als je een doos van formaat A als het origineel neemt,
• k = ³√(540 ÷ 150) = ³√3,6 ≈ 1,533

→ De lengte van een doos van formaat B = k × de lengte van een doos van formaat A = ³√3,6 × 8 ≈ 12,26 cm.

→ De lengte van een doos van formaat B is 12,3 cm (rond af op één decimaal). 

b.

→ De hoeveelheid karton die nodig is voor de dozen betreft de oppervlakte van de dozen.

• oppervlakte beeld = k² × oppervlakte origineel
• hoeveelheid karton voor een doos van formaat B = k² × hoeveelheid karton voor een doos van formaat A = (³√3,6)² × hoeveelheid karton voor een doos van formaat A
• (³√3,6)² ≈ 2,349

→ Voor een doos van formaat B is 2,35 keer zoveel karton nodig als voor een doos van formaat A (rond af op twee decimalen). 

c.

→ Voor een doos van formaat C is tien keer zoveel karton nodig als voor een doos van formaat A.

• hoeveelheid karton voor een doos van formaat C = k² × hoeveelheid karton voor een doos van formaat A 
• k² = 10
• k =√10

→ Het gewicht van drop die gaat in een doos van formaat C:

• inhoud beeld = k³ × inhoud origineel
• Het gewicht van drop die gaat in een doos van formaat C = k³ × het gewicht van drop die gaat in een doos van formaat A = (√10)³ × 150 gram ≈ 4743,41 

→ Het gewicht van drop die gaat in een doos van formaat C is 4740 gram (rond af op tientallen).

Opgave 6.

a.

• Raam A: ① rechthoekig, ② 80 cm hoog en ③ de oppervlakte 4000 cm²
• Raam B: ① een verkleining van raam A en ② de oppervlakte 250 cm² 

→ De vergrotingsfactor k:

• oppervlakte beeld = k² × oppervlakte origineel
• k = √(oppervlakte beeld ÷ oppervlakte origineel) = √(250 ÷ 4000) = 0,25

→ De hoogte van raam B = k × de hoogte van raam A = 0,25 × 80 = 20 cm

→ De breedte van raam B = k × de breedte van raam A = 0,25 × 50 = 12,5 cm

• De breedte van raam A = 4000 cm² ÷ 80 cm = 50 cm

b.

• Muur A: ① 3,2 meter bij 3,8 meter, ② voor muur A is 2,6 liter verf nodig 
• Muur B: ① een vergroting van muur A, ② voor muur B is 16,25 liter verf nodig

→ De vergrotingsfactor k:

• oppervlakte beeld = k² × oppervlakte origineel
• Pas op: de verf wordt gebruikt voor de oppervlakte van de muur.
• k = √(oppervlakte beeld ÷ oppervlakte origineel) = √(16,25 ÷ 2,6) ≈ 2,5

→ De breedte van muur B = k × de breedte van muur A = 2,5 × 3,8 meter = 9,5 meter

→ De hoogte van raam B = k × de hoogte van raam A = 2,5 × 3,2 meter = 8 meter

Opgave 7.

→ De inhoud van de sneeuwbal is met 75% afgenomen. 

→ De inhoud van de gesmolten sneeuwbal = 25% van de inhoud van de originele sneeuwbal

• inhoud beeld = k³ × inhoud origineel
• k³ = 25% = 0,25
• k = ³√0,25 ≈ 0,630
• de straal van de gesmolten sneeuwbal = k × de straal van de originele sneeuwbal
• percentuele afname = (afname ÷ OUD) × 100 %  ← Zie: H6. blz.59 
• OUD = de staal van de originele sneeuwbal
• afname = de straal van de originele sneeuwbal – de straal van de gesmolten sneeuwbal 

                                 = de straal van de originele sneeuwbal – (k × de straal van de originele sneeuwbal)
                                 = de straal van de originele sneeuwbal(1 – k)  

                                                     ↑

                                   ontbinden in factoren, gemeenschappelijke factor, Zie H7 blz. 107 

• afname ÷ OUD = {de straal van de originele sneeuwbal(1– k)} ÷ de straal van de originele sneeuwbal = 1– k
• percentuele afname = (1 – k) × 100% = (1 – 0,630) × 100% = 0,370 × 100% = 37,0%

→ De straal van de sneeuwbal is met 37,0% afgenomen.